www.ikes.16mb.com

Version 220319

Inductors in AC circuits

Introduction to the sine wave formula



An alternating current can be represented by

I = I0sin(ωt),

where I0 is the amplitude of the current and ω = 2π×frequency

For an ideal resistor, using Ohm's Law, the alternating voltage across a resistor, R, is give by

V = R×I0sin(ωt),

As can be seen from the current and voltage formulae, they are always in phase.


For an ideal inductor, the induced voltage across an inductor when a current, I, is passing is given by Faraday's Law

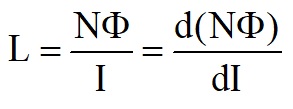
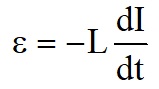
This voltage opposes the voltage causing the current to flow through the inductor.

So for an ideal inductor, the applied voltage, V, must be equal and opposite to this induced voltage.

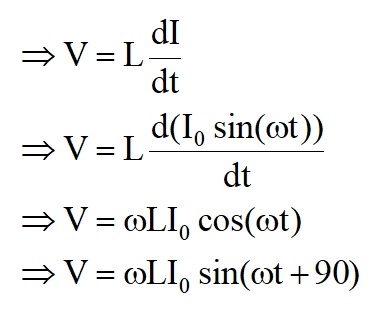
This expression shows that the applied voltage across an inductor leads the current by 90° (π/2 radians).


For an ideal inductor, the ratio of the applied voltage to the current passing through is called the reactance, XL.
This should be compared to Ohm's law where the ratio of voltage to current is called resistance.

XL = ωL

As can be seen from the formula, inductive reactance increases linearly with frequency.


An inductor and resistor in series.

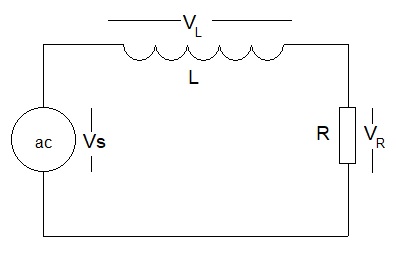
The current passing in the circuit is

I = I0sin(ωt),

and is the same through both the resistor and inductor as they are in series.

=> The voltage across the resistor, R, is

VR = RI0sin(ωt),

and is in phase with the current.
=> The voltage across the inductor, L, is

VL = ωLI0sin(ωt + 90),

=> The voltage across the inductor leads the current by 90° (π/2 radians)

To make sense of what this means, it is helpful to represent these voltages and currents on a diagram.

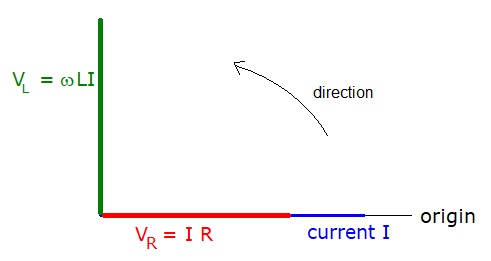
Kirchhoff's 2nd Law states that the algebraic sum of the potential differences in any loop must equal zero. (Conservation of energy)
Since VL and VR are not in phase they must be added as vectors.

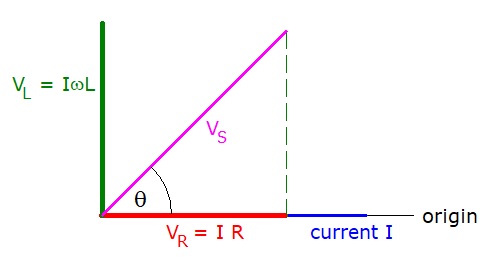
Looking at the final term and comparing to Ohm's Law, √(R2 + XL2) represents the opposition to the current from the power supply.
Containing both resistance and reactance, it is called the Impedance of the circuit with the symbol Z.

Z = √(R2 + XL2)

The power supply voltage is out of phase with the current by angle θ, where tanθ = VL/VR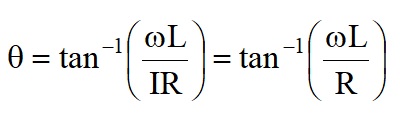

The angle θ is often referred to as the phase angle.


AC Circuits in Complex Form
It is very convenient to use Complex numbers for processing AC calculations.

The real axis represents Resistance.   Power is only dissipated in pure (real) resistance.

The imaginary axis represents Reactance.   Power is NOT dissipated in reactance (averaged over a time period).

Unfortunately, i is the symbol used to represent current.
To avoid confusion in circuit calculations, j is used to represent √(-1)

Inductive reactance, XL, becomes jωL

RL Potential Divider

The basic resistor Potential Divider formula is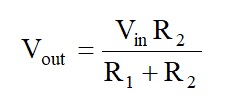

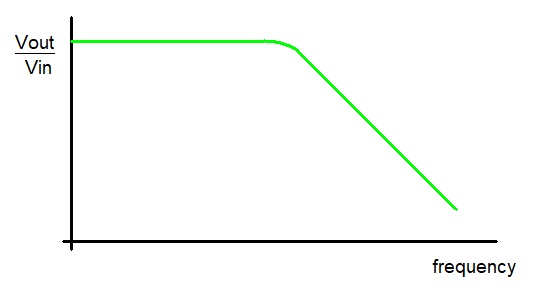
Applying this to the circuit below

=> when ω is small,   Vout/Vin ≈ 1 and

when ω is large,   Vout/Vin ≈ 1/ωL

This circuit works as a simple 'Low Pass filter' - it attenuates high frequencies but passes low frequencies.


If the inductor and resistor swap places in the circuit above, it is worth verifying that a High Pass filter is formed.