
AC Circuits in Complex Form
Introduction
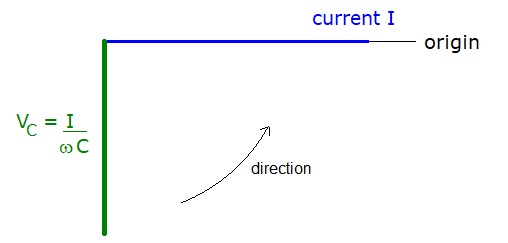
The alternating voltage across a capacitor lags the current passing through by 90° (π/2 radians).
This can be represented by the diagram below.
A complex number consists of a real part and an imaginary part and is represented by a Z.
In mathematics, the imaginary part is designated by an i, where i represents √(-1).
In Cartesian form, the 'x' axis represents the real component and the 'y' axis the imaginary component of a complex number.
The diagram below represents a complex number with a real component of a and an imaginary component of b.

The complex number, Z, would then be Z = a + ib.
Addition and Subtraction of complex numbers.
The real and imaginary components are processed separately, e.g.(a + ib) + (c + id) = (a+c) + i(b + d).
Similarly for subtraction(a + ib) - (c + id) = (a-c) + i(b - d).
Multiplication and Division of complex numbers.
For multiplication, the brackets are processed as with normal algebra e.g.(a + ib) × (c + id) = (ac-bd) + i(ad+bc).
Division is more interesting and is achieved by making the divisor into a real number, e.g.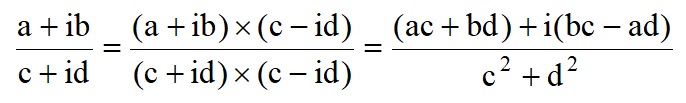
Magnitude of a complex number.
This is the distance the complex number is from the origin on an Argand diagram.For the complex number Z = a + ib,
The magnitude, |Z| = √(a2 + b2)
Arguement of a complex number.
This is the angle to the complex number measured from the positive real axis on an Argand diagram.For the complex number Z = a + ib,
The arguement, arg(Z) = tan-1(imag/real) = tan-1(b/a)
Application to AC Circuits.
Complex numbers are very convenient for processing AC calculations.The real axis represents Resistance. Power is only dissipated in pure (real) resistance.
The imaginary axis represents Reactance. Power is NOT dissipated in reactance (averaged over a time period).
Unfortunately, i is the symbol used to represent current.
To avoid confusion in circuit calculations, j is used to represent √(-1)