www.ikes.16mb.com

Version 220319

Basic Sine Wave

Sine function.

The green line has unity length and is at an angle of θ to the origin.
The projection of the green line onto the value axis has a length V = sin(θ).

Now consider the green line rotating at a constant angular speed, ω, about 0, as in the diagram below.

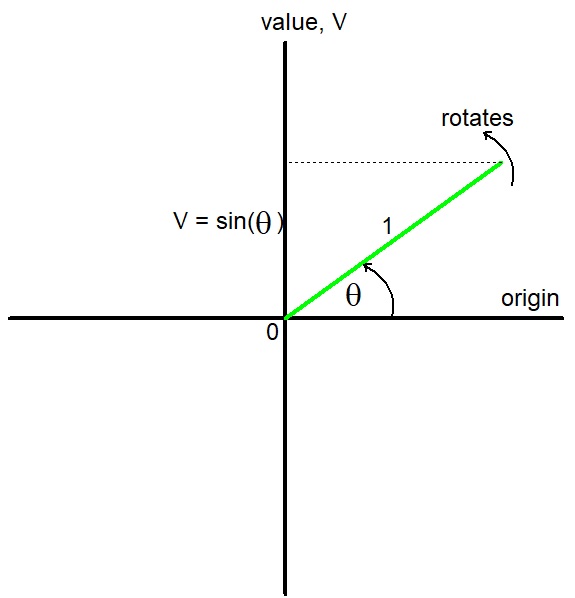
The projection of the green line on the value axis will now vary with time, t, and θ = ωt

so => V = sin(ωt)

If the green line does one complete revolution in time T (time period), then 2π = ωT and

so => V = sin(2πt/T)

But frequency, f, is equal to 1/T, so ω = 2πf

so => V = sin(2πft)

or the equation could be left as V = sin(ωt), where ω is the 'angular frequency' = 2πf

To make the value of V larger than 1, the length of the green line is multiplied by a constant, V0

=> V = V0sin(ωt)   or   V = V0sin(2πft)


A graph of V against time is shown below.