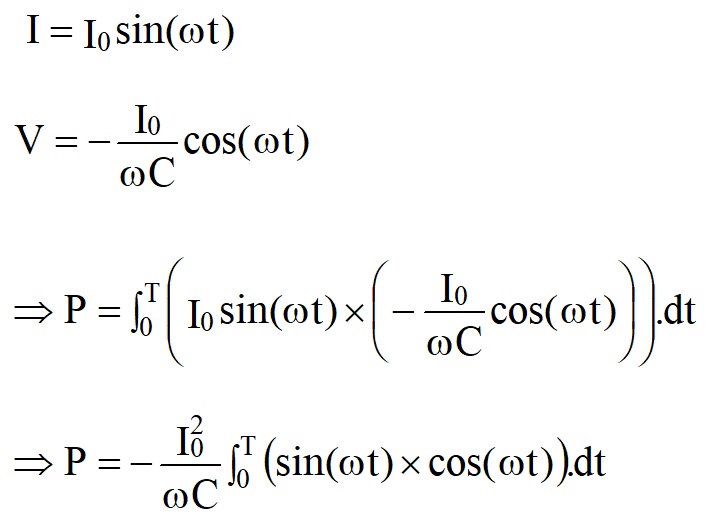Power from Alternating Current
W = Q×V
Electric current, (I), is the charge, (Q), flowing per unit time, (t).=> Q = I×t
Combining these equations together gives=> W = I×t×V
Power, (P) is the energy, (W), per unit time, (t)=> P = I×V
For a resistor
Ohm's Law gives V = I×R=> P = I×V = I2×R = V2/R
Introduction to the sine wave formula
For a sine wave alternating voltage, V = V0sin(ωt), and the power dissipated in a resistor R over one time period, (T) is
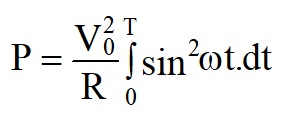
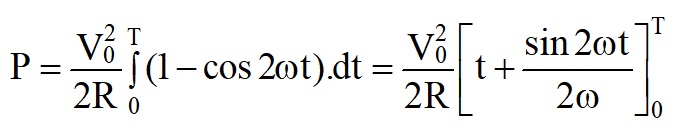
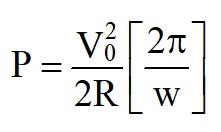
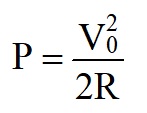
This quantity is known as the root mean square (rms) voltage.
For a capacitor
Introduction to capacitors in AC circuits
Using P = I × V and summing over one time period