www.ikes.16mb.com

Version 220319

Lens Revision

Introduction.

The eye (and brain) is used to light travelling in straight lines and interprets what we see as such.

A ray of light represents the direction of travel of light between two points in space.

Lenses are shaped pieces of material which cause light to be refracted in specific directions.
Light rays travelling through a lens all take the same time. (Fermat's Principle)

Types of lens.

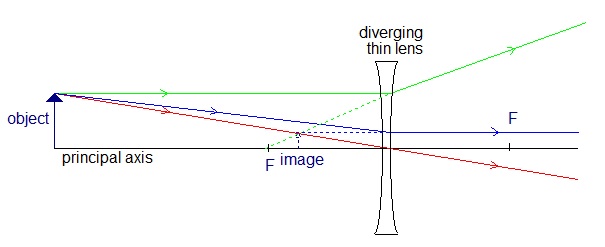
There are two main types of lens:-
- Converging, where parellel rays of light are refracted to bend inwards and cross
- Diverging, where parellel rays of light are refracted to bend outwards and never cross

Converging lenses are thicker in the middle than at the edges.

Diverging lenses are thinner in the middle than at the edges.


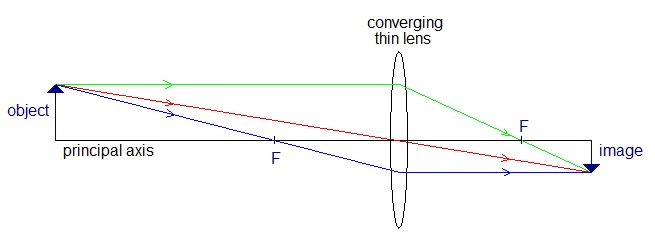
Construction Rays for 'Thin' converging lenses.

There are three distinct paths that rays of light can travel through a lens.
- 1). - Through the optical centre of the lens.   This ray continues in a straight line.
        A special case of this ray is when it is at right angles to the lens.
        This ray is known as the Principal Axis.
- 2). - At right angles to the lens.   The ray is refracted to pass through the 'Focus'.
- 3). - Through the focus towards the lens.   The ray is refracted to be at right angles to the lens.

Definitions.

- Optical centre - The point on a thin lens where rays of light are not refracted.
- Principal axis - The path of a ray of light travelling at right angles to, and towards the optical centre of the lens, passes.
- Focus - the point on the principal axis where rays of light travelling parallel to the principal axis cross or appear to cross.
- Object - the source of light being viewed through the lens.
- Image - what is observed after the light from the object has passed through the lens.
- Focal length, f - the distance of the Focus from the lens.
- Object distance, u - the distance of the Object from the lens.
- Image distance, v - the distance of the Image from the lens.
- Object height, o - height of the object.
- Image height, i - height of the image.
- Real - A real object/image can be 'touched' - rays of light come from the object/image.
- Virtual - A virtual object/image cannot be 'touched' - rays of light only appear to come from the object/image.

Measurements associated with real objects/images (e.g. u, v) are positive numbers.
Measurements associated with virtual objects/images (e.g. u, v) are negative numbers.

Power of a lens.

The power of a lens is defined as the reciprocal of the focal length of the lens when measured in metres.
The power of a lens is measured in Dioptres (D) and is positive for a converging lens and negative for a diverging lens.
A converging lens with a focal length of 100mm (0.1m) will therefore have a power of 1/0.1 = +10D.

Linear Magnification.

How many time larger the image is than the object = i/o.

From the diagram, tanα = o/u = i/v   => Linear magnification, i/o = v/u

Thin lens formula.

Derivation - consider the diagram below.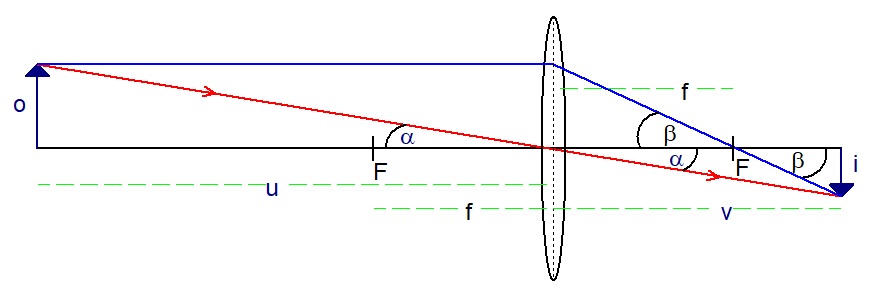

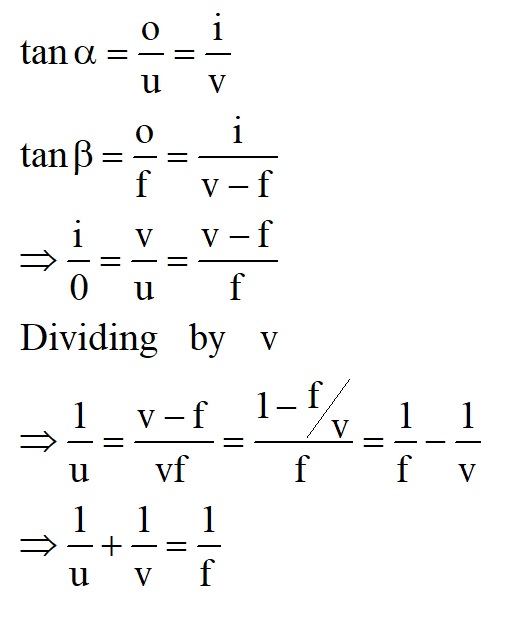
The thin lens formula should be used with the 'real is positive' sign convention.

Scale diagrams.

Graph paper helps
Choose a sensible scale and state it on the diagram
Remember 1mm does not equal 1cm, but can represents it!!!

Object/Image descriptors.

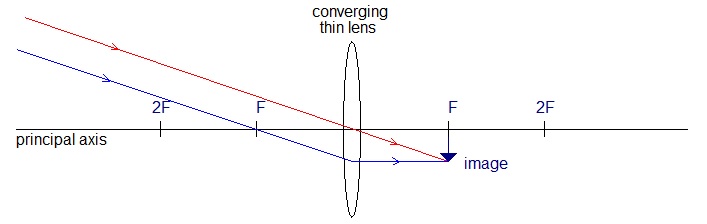
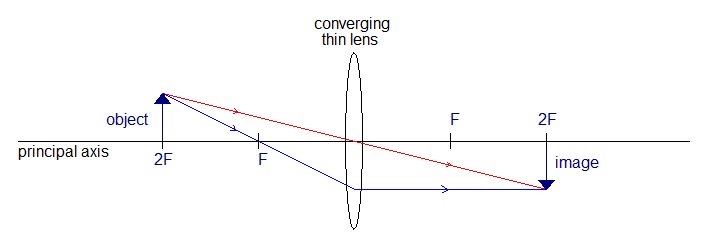
- magnified - enlarged - diminished - smaller - upright - erect - inverted - real - virtual

Standard ray diagrams.

Identify applications for each of these cases.
Describe the image in each case.

 

 

 


 


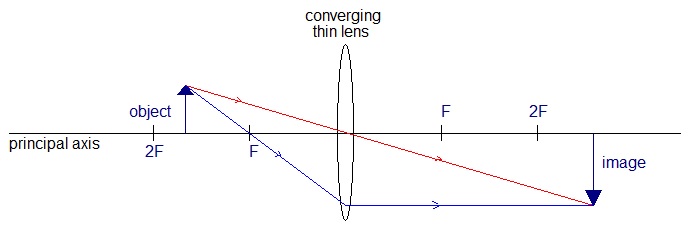
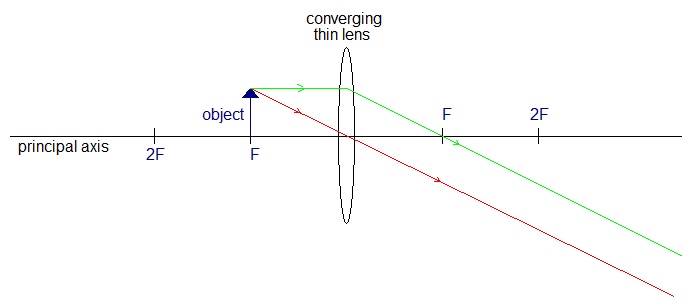
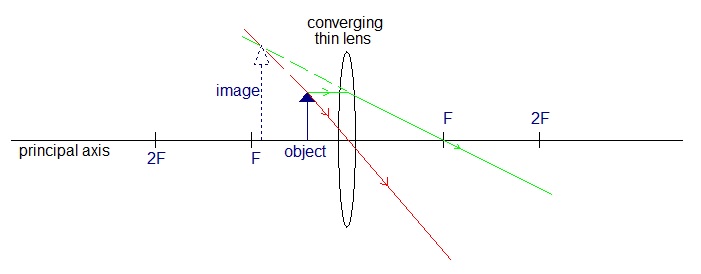
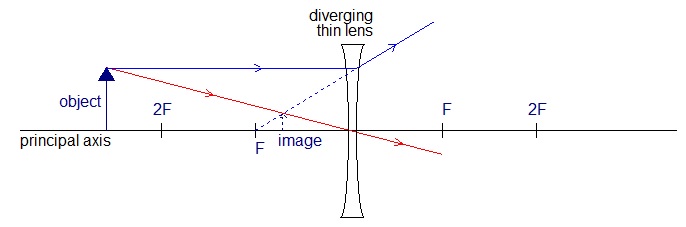
Measuring the focal length of a converging lens.

1). An approximate method using a distant object.
2). An accurate method using the lens formula.

Lens aberrations.

Spherical - Parallel rays close to the principal axis cross at a different place to those further from the principal axis.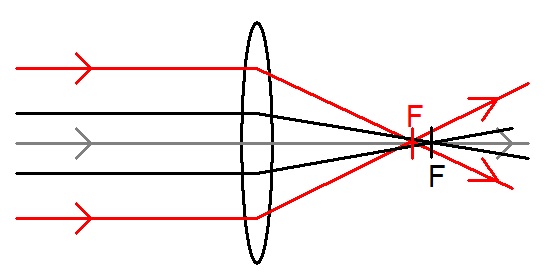

Chromatic - Different colours of light are refracted by different amounts.




Questions.

NOTE   Assume all lenses are thin unless otherwise stated.

1). (a) A small object is placed on the axis of a converging lens of focal length 10cm so that it is 15cm from the lens.
        Calculate the position of the image.
    (b) The object is now moved so that it is 5cm from the lens.
        Calculate the new position of the image
        Calculate how many times larger than the object the image now is.

2). A simple magnifying glass produces an enlarged erect image when an object is placed 10cm from the lens.
If the length of the image is twice that of the object, calculate:
        (a) the distance of the image from the lens,
        (b) the focal length of the lens.

3). An object 1mm tall is placed 2.9cm from a convex lens of focal length 3cm so that it is perpendicular to,
and has one end resting on, the principal axis of the lens. Calculate:-
        (a) the position of the image.
        (b) the size of the image.

4). An object 4cm high is at right angles to the principal axis of a diverging lens of focal length 20cm and at 30cm from it.
        Determine the position of the image and its size.

5). A convex lens of focal length 12cm is used to produce a real image of an object enlarged four times.
        Determine how far must the object be placed from the lens.

6). If the focal length of a camera lens is 20cm, how far away from the sensor
must the lens be set in order to photograph an object 100cm from the lens?

7). A data projector has an LCD screen 1.8cm by 1.2cm.
When the projector is 5m from the screen it produces an image 3.6m by 2.4m.
        Calculate the focal length of the projection lens.

8*). A long sighted person has long distance glasses of focal length 1.5m and reading glasses of focal length 90cm.
To see tiny items the person sometimes wears both pairs of glasses at the same time.
        (a) Show that, for thin lenses placed very close together, the power of the combination is equal to the sum of the powers of each lens.
        (b) Calculate the focal length and power of the combined pairs of glasses.

9*). A photographer wants to convert his camera lens of focal length 100mm into a telephoto lens of focal length 600mm.
        Calculate the focal length of the lens that he should place next to his camera lens to achieve this.

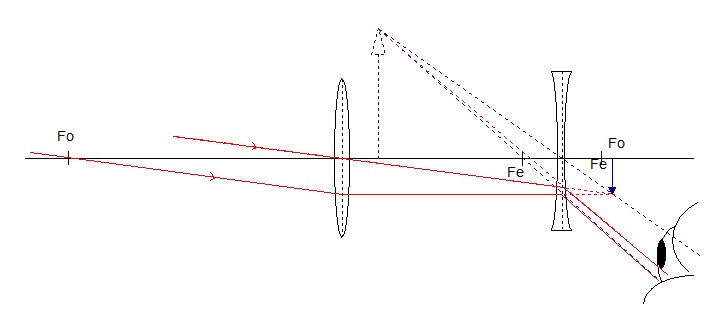
10*). A Newtonian telescope consists of a converging objective lens of focal length 400mm and a converging eye piece lens of focal length 20mm.
The final image is to be virtual and 250mm from the eyepiece lens.
        (a) Draw a ray diagram of the arrangement.
        (b) Calculate the distance between the objective and eyepiece lenses.
        (c) Calculate the distance of the 'eye ring' from the eyepiece lenses.
        (d) Explain why this is the best position for the observer's eye.
        (e) Calculate the angular magnification of the final image.

11*). A Galilean telescope consists of a converging objective lens of focal length 500mm and a diverging eye piece lens of focal length 50mm.
The final image is to be real and 250mm from the eyepiece lens.
        (a) Draw a ray diagram of the arrangement.
        (b) Calculate the distance between the objective and eyepiece lenses.
        (c) Calculate the angular magnification of the final image.

12*). A microscope has a 10mm objective lens and a 30mm eyepiece lens.
An object is placed 12mm from the objective lens and a virtual image is formed 250mm from the eye.
        (a) Draw a ray diagram of the arrangement.
        (b) Calculate the distance between the objective and eyepiece lenses.
        (c) Calculate the magnification of the final image.



Drawing ray diagrams for telescopes and microscopes.

- 1). Start with the eyepiece lens and where you want the final image to be.
- 2). Use construction rays to locate the position for the eyepiece object.
- 3). Add the objective - use construction rays to locate the objective object.

Newtonian telescope with image at near point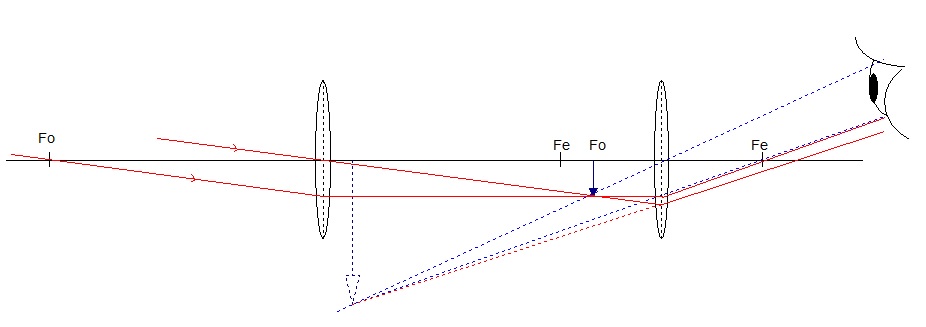

Galilean telescope with image at near point