
Motion and Projectiles
Aristotle
The answer depends on how the question is asked.- Why does the object not continue to move? - What makes the object stop?
Galileo
Newton
Laws of Motion
Newton 1
Every body continues in its present state of rest or uniform motion unless acted upon by an (external) resultant force
If F = 0 then Δv = 0
Video - table cloth (†)Newton 2
The rate of change of momentum is proportional to the applied force and takes place in the direction of that force
F = Δmv/Δt
Impulse = Force × Δt = Δmv
Newton 3
To every reaction there is an equal and opposite reaction
Conservation of momentum
p before = p after
- act on different bodies
- have the same magnitude
- act in opposite directions
- are the same type
Terms
Distance - Displacement
Speed - Velocity rate of change of distance - rate of change of displacement
acceleration rate of change of velocity
s = displacement, u = initial velocity, v = final velocity, a = acceleration, t = time
Uniform acceleration
One dimension - no accelerationdistance = speed × time
One dimension - uniform acceleration
v = u + at
s = ut + ½at2
v2 = u2 + 2as
s = ½(v+u)t
s = vt - ½at2
Motion Graphs
Gradient of displacement time graph is velocity. (ms-1)Area under velocity time graph is displacement. (m)
Gradient of velocity time graph is acceleration. (ms-2)
Stroboscope photos, video recordings, light gates etc
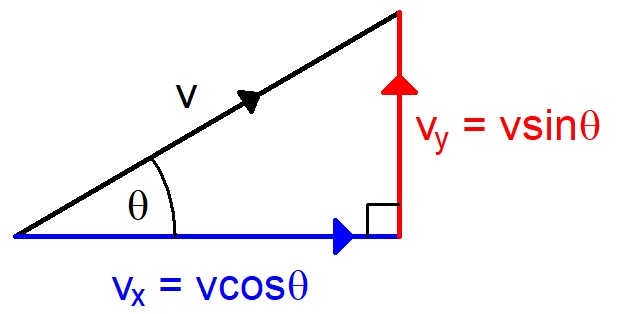
Resolving vectors
Resolve to find the horizontal and vertical components.BEWARE of the vertical angle!
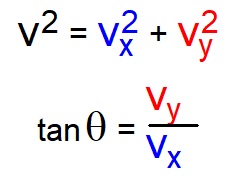
Projectiles
Horizontal and vertical velocities are independent.Vertical motion is that of gravity,
- assuming no friction or air resistance - standard SUVAT equations.
- at maximum height, vertical velocity = 0
Horizontal motion is constant,
assuming no friction or air resistance.

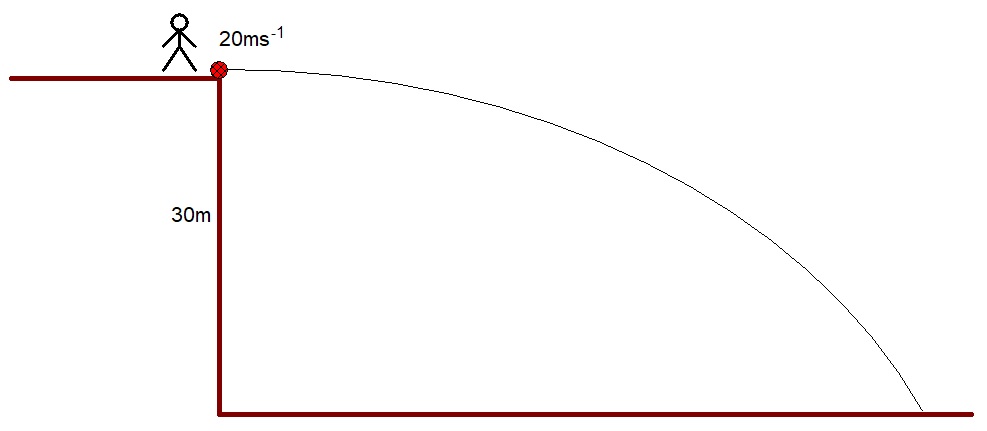
E.g. 1 - A ball is kicked horizontally from the top of a vertical cliff, 30m high, with a horizontal velocity of 20ms-1.
Ignoring air resistance, calculate:
- (a) the time taken for the ball to hit the ground,
- (b) the distance from the base of the cliff to where the ball lands, (the range)
- (c) the velocity that the ball hits the ground with.
Variations:-
E.g. 2 - A food parcel is to be dropped by an aeroplane flying at a height of 500m and a speed of 100ms-1.
Ignoring air resistance, calculate how far ahead of the target the food parcel must be released from the aeroplane.
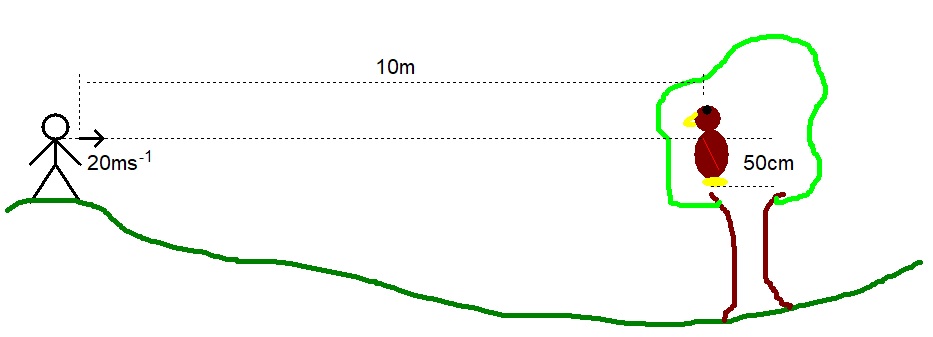
E.g. 3 - A hunter sees a bird sitting on a tree branch directly opposite as in the diagram below and fires an arrow horizontally with a velocity of 20ms-1.
Type 2 - initial vertical and horizontal velocities, level ground - (initial velocity = final velocity).
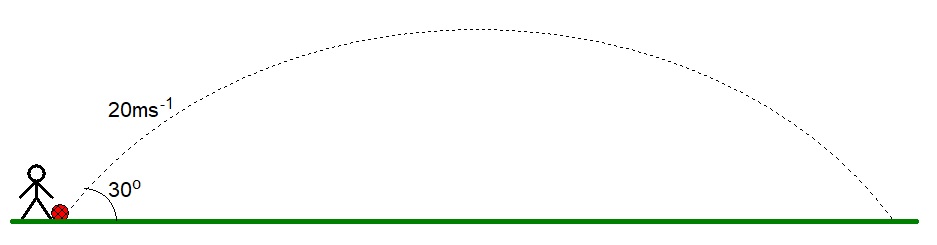
E.g. 4 - A ball is kicked upwards at an angle of 30° from the ground, with a velocity of 20ms-1.
Ignoring air resistance, calculate:
- (a) the time taken for the ball to hit the ground,
- (b) the maximum height of the ball,
- (c) the range,
- (d) the velocity that the ball hits the ground with.
- (d) What angle must the ball be kicked at to give the maximum range?
Variations:-
E.g. 5 - A rocket is fired upwards at an angle of 30° to the vertical, with a velocity of 200ms-1.
Ignoring air resistance, calculate:
- (a) the maximum height of the rocket,
- (b) how far from the launch site it will land.
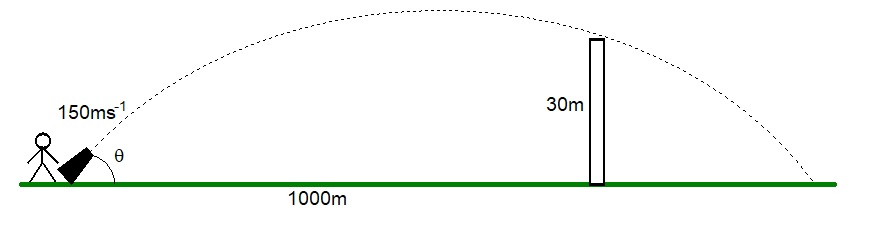
E.g. 6 - A castle wall is 30m high and 1km away from a cannon.
A cannon ball has a muzzle velocity of 150ms-1.
At what angle(s) must the cannon ball be fired so that it just passes over the top of the castle wall?
(Ignore air resistance.)
Type 3* - initial vertical and horizontal velocities, changing ground level.
E.g. 7 - A ball is kicked upwards at an angle of 60° to the vertical, with a velocity of 20ms-1.
The ground slopes away at an angle of -10° to the horizontal.
Ignoring air resistance, calculate:
- (a) the maximum height of the ball above the ground,
- (b) the time taken for the ball to hit the ground,
- (c) the range,
- (d) the velocity that the ball hits the ground with.
- (d) What angle must the ball be kicked at to give the maximum range?
