www.ikes.16mb.com

Version 220319

Capacitors in DC circuits
Capacitor charging.

Adding the potential differences:

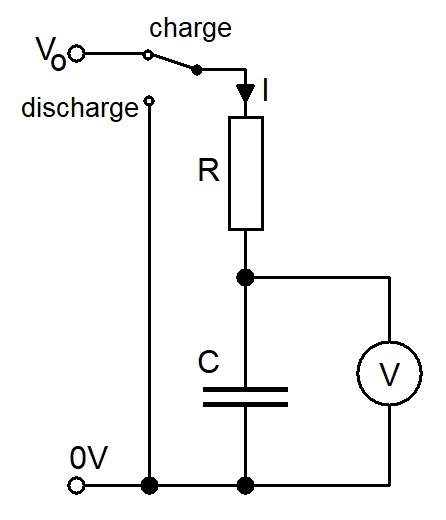
V0 = IR + V

But Q = CV

=> V0 = IR + Q/C

But I = dQ/dt

since Q0 = CV0

Rearranging for V

As can be seen from this formula, the product of R and C has units of time. (Exponents must have no units.)
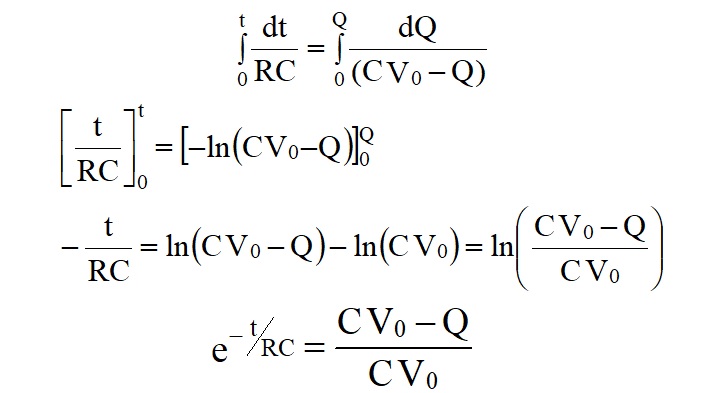
The quantity RC is called the Time Constant.
Show that the voltage across the capacitor after one time constant ≈ 63% V0

To fully charge the capacitor takes a very long time.
It is normal to assume that the capacitor has fully charged after five time constants

t = 5RC

by which time the capacitor has charged to 99.3% of V0.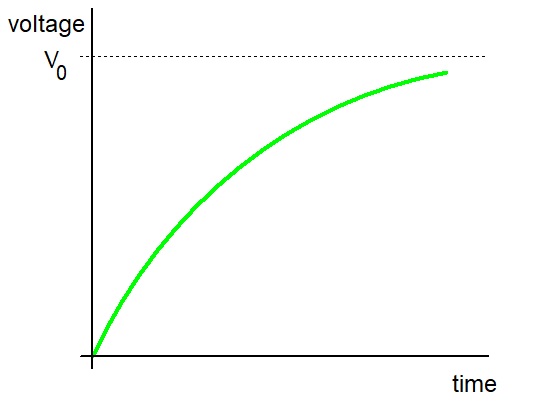



Differentiating this formula

gives

Setting t = 0, will give the gradient of the graph at the origin which enables the value of the capacitor to be calculated
by measuring the gradient.


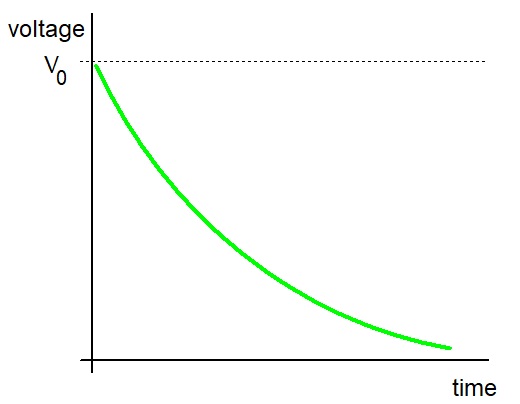
Discharging

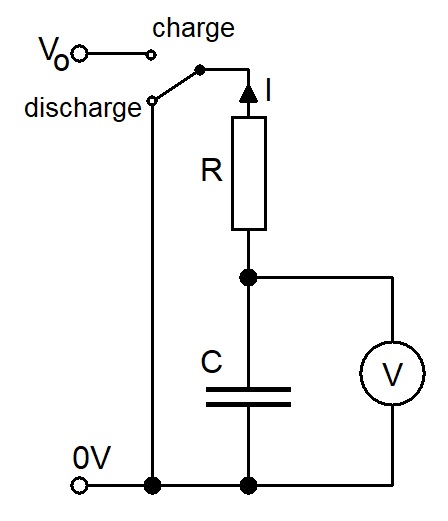
When the switch is moved from the charge to discharge position, the capacitor begins to discharge through R.
The supply voltage, V0, has been replaced by 0V.

=> 0 = IR + V

But Q = CV

=> 0= IR + Q/C

But I = dQ/dt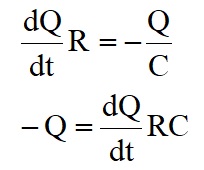

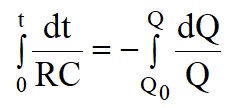
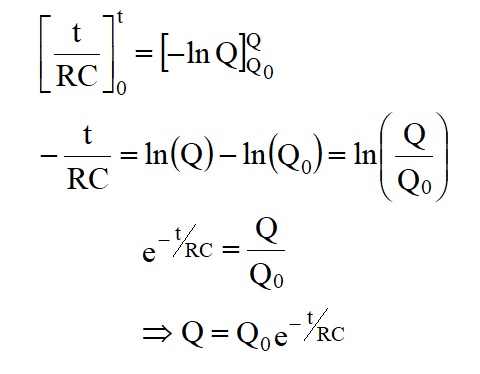
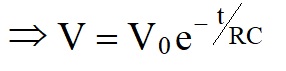
since Q0 = CV0 and Q = CV

The voltage across the capacitor after one time constant:

V = V0e-1 = 0.368V0

=> after one time constant, the capacitor has discharged to ≈37% of the initial voltage.
To fully discharge the capacitor takes a very long time.
It is normal to assume that the capacitor has fully discharged after five time constants

t = 5RC

by which time the capacitor has discharged to≈ 0.7% of V0.


Energy stored in a capacitor

From the definition of Potential Difference, Energy = charge × potential difference, W = q × V
For each additional quantity of charge, Δq the capacitor gains while charging, an additional ΔW energy is gained.

ΔW = V Δq

But Q = C × V

=> ΔW = V CΔV

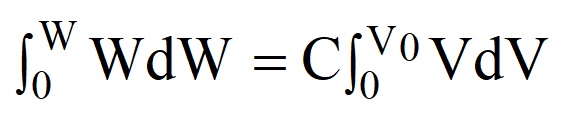
=> W = ½CV2

NOTE
Only half the energy that left the power supply is actually stored within the capacitor,
the other half is dissipated within the series resistor.